HP OpenVMS SystemsBASIC |
Compaq BASIC for OpenVMS
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Previous | Contents | Index |
BASIC expressions consist of operands (constants, variables, and functions) separated by arithmetic, string, relational, and logical operators.
The following are types of BASIC expressions:
BASIC evaluates expressions according to operator precedence and uses the results in program execution. Parentheses can be used to group operands and operators, thus controlling the order of evaluation.
The following sections explain the types of expressions you can create
and the way BASIC evaluates expressions.
1.6.1 Numeric Expressions
Numeric expressions consist of floating-point, integer, or packed decimal operands separated by arithmetic operators and optionally grouped by parentheses. Table 1-7 shows how numeric operators work in numeric expressions.
| Operator | Example | Use |
|---|---|---|
| + | A + B | Add B to A |
| -- | A -- B | Subtract B from A |
| * | A * B | Multiply A by B |
| / | A / B | Divide A by B |
| ^ | A^B | Raise A to the power B |
| ** | A**B | Raise A to the power B |
In general, two arithmetic operators cannot occur consecutively in the same expression. Exceptions are the unary plus and unary minus. The following expressions are valid:
A * + B A * - B A * (-B) A * + - + - B |
The following expression is not valid:
A - * B |
An operation on two numeric operands of the same data type yields a result of that type. For example:
| A% + B% | Yields an integer value of the default type |
| G3 * M5 | Yields a floating-point value if the default type is REAL |
If the result of the operation exceeds the range of the data type, BASIC signals an overflow error message.
The following example causes BASIC to signal the error "Integer error or overflow" because the sum of A and B (254) exceeds the range of -128 to +127 for BYTE integers. Similar overflow errors occur for REAL and DECIMAL data types whenever the result of a numeric operation is outside the range of the corresponding data type.
DECLARE BYTE A, B A = 127 B = 127 PRINT A + B END |
It is possible to assign a value of one data type to a variable of a different data type. When this occurs, the data type of the variable overrides the data type of the assigned value. The following example assigns the value 32 to the integer variable A% even though the floating-point value of the expression is 32.13:
A% = 5.1 * 6.3 |
The following sections describe the floating-point and integer promotion rules for VAX BASIC and Alpha BASIC, unless otherwise noted.
When an expression contains operands with different data types, the data type of the result is determined by BASIC data type promotion rules:
Note that BASIC performs sign extension when converting BYTE, WORD, and LONG integers to a higher INTEGER data type (WORD, LONG, or QUAD). The high order bit (the sign bit) determines how the additional bits are set when the BYTE, WORD, or LONG is converted to WORD, LONG, or QUAD. If the high order bit is zero (positive), all higher-order bits in the converted integer are set to zero. If the high order bit is 1 (negative), all higher-order bits in the converted integer are set to 1.
Data Type Results in VAX BASIC Expressions
The following chart lists the data type results possible for VAX BASIC in numeric expressions that combine different data types.

For example, if one operand is SINGLE and one operand is DOUBLE, BASIC promotes the SINGLE value to DOUBLE, performs the specified operation, and returns the result as a DOUBLE value. This promotion is necessary because the SINGLE data type has less precision than the DOUBLE value, whereas the DOUBLE data type can represent all possible SINGLE values.
The data types BYTE, WORD, LONG, SINGLE, and DOUBLE form a simple hierarchy: if all operands in an expression are of these data types, the result of the expression is the highest data type used in the expression.
When the operands are DOUBLE and GFLOAT, BASIC promotes both values to HFLOAT, and returns an HFLOAT value. The promotion of DOUBLE and GFLOAT to HFLOAT is necessary because a DOUBLE value is more precise than a GFLOAT value, but cannot contain the largest possible GFLOAT value. Consequently, BASIC promotes these data types to a data type that can hold the largest and most precise value of either operand.
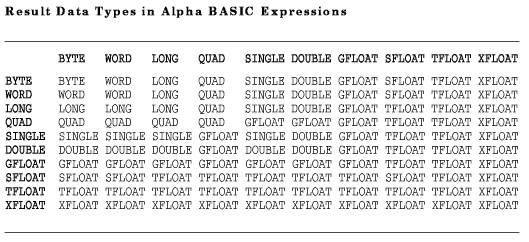
Data Type Results in Alpha BASIC
The following chart shows the data type of the result of an operation that combines arguments of differing data types. Alpha BASIC first promotes, if necessary, the arguments to the result data type, and then performs the operation.
Alpha BASIC does not support HFLOAT.
BASIC allows the DECIMAL(d,s) data type. The number of digits (d) and the scale or position of the decimal point (s) in the result of DECIMAL operations depends on the data type of the other operand. If one operand is DECIMAL and the other is DECIMAL or INTEGER, the d and s values of the result are determined as follows:
DECLARE DECIMAL(5,2) A DECLARE DECIMAL(4,3) B |
Note that only INTEGER data types are converted to the DECIMAL data type. If one operand is DECIMAL and one is floating-point, the DECIMAL value is converted to a floating-point value. The total number of digits in (d) in the DECIMAL value determines its new data type, as shown in Table 1-8 for VAX BASIC and Table 1-9 for Alpha BASIC.
| Number of DECIMAL Digits |
Floating-Point Operands | |||
|---|---|---|---|---|
| in Operand | SINGLE | DOUBLE | GFLOAT | HFLOAT |
| 1-6 | SINGLE | DOUBLE | GFLOAT | HFLOAT |
| 7-15 | DOUBLE | DOUBLE | GFLOAT | HFLOAT |
| 16 | DOUBLE | DOUBLE | HFLOAT | HFLOAT |
| 17-31 | HFLOAT | HFLOAT | HFLOAT | HFLOAT |
For example, if the value of d is from 7 to 15, the operand is converted to:
Thus, a DECIMAL(8,5) operand is converted to DOUBLE if the other operand is SINGLE or DOUBLE, to GFLOAT if the other operand is GFLOAT, and to HFLOAT if the other operand is HFLOAT. Note also that exponentiation of a DECIMAL data type returns a REAL value.
For Alpha BASIC, if one argument is DECIMAL data type and one is a floating point data type, the DECIMAL data type argument is first converted to a floating point data type as follows in Table 1-9.
| Number of DECIMAL Digits |
Floating-Point Operands | |||||
|---|---|---|---|---|---|---|
| in Operand | SINGLE | DOUBLE | GFLOAT | SFLOAT | TFLOAT | XFLOAT |
| 1-6 | SINGLE | DOUBLE | GFLOAT | SFLOAT | TFLOAT | XFLOAT |
| 7-15 | DOUBLE | DOUBLE | GFLOAT | TFLOAT | TFLOAT | XFLOAT |
| 16 | DOUBLE | DOUBLE | GFLOAT | XFLOAT | XFLOAT | XFLOAT |
| 17-31 | GFLOAT | GFLOAT | GFLOAT | XFLOAT | XFLOAT | XFLOAT |
GFLOAT maintains up to 15 digits of precision. Mixing DECIMAL items containing 16 or more bits with GFLOAT items may cause a loss of precision.
Operations performed on DOUBLE operands are performed in GFLOAT. When
the operation is complete, the GFLOAT result is converted to DOUBLE.
Therefore, it is possible to lose three binary digits of precision in
arithmetic operations using DOUBLE.
1.6.2 String Expressions
String expressions are string entities separated by a plus sign (+). When used in a string expression, the plus sign concatenates strings. For example:
INPUT "Type two words to be combined";A$, B$ C$ = A$ + B$ PRINT C$ END |
Output
Type two words to be combined? long ? word longword |
Conditional expressions can be either relational or logical expressions. Numeric relational expressions compare numeric operands to determine whether the expression is true or false. String relational expressions compare string operands to determine which string expression occurs first in the ASCII collating sequence.
Logical expressions contain integer operands and logical operators.
BASIC determines whether the specified logical expression is
true or false by testing the numeric result of the expression. Note
that in conditional expressions, as in any numeric expression, when
BYTE, WORD, and LONG operands are compared to WORD, LONG, and QUAD, the
specified operation is performed in the higher data type, and the
result returned is also of the higher data type. When one of the
operands is a negative value, this conversion will produce accurate but
perhaps confusing results, because BASIC performs a sign
extension when converting BYTE and WORD integers to a higher integer
data type. See Section 1.6.1.1 for information about integer conversion
rules.
1.6.3.1 Numeric Relational Expressions
Operators in numeric relational expressions compare the values of two operands and return either -1 if the relation is true (as shown in Example 1), or zero if the relation is false (as shown in Example 2). The data type of the result is the default integer type.
A = 10 B = 15 X% = (A <> B) IF X% = -1% THEN PRINT 'Relationship is true' ELSE PRINT 'Relationship is false' END IF |
Output
Relationship is true |
A = 10
B = 15
X% = A = B
IF X% = -1%
THEN PRINT 'Relationship is true'
ELSE
PRINT 'Relationship is false'
END IF
|
Output
Relationship is false |
Table 1-10 shows how relational operators work in numeric relational expressions.
| Operator | Example | Meaning |
|---|---|---|
| = | A = B | A is equal to B. |
| < | A < B | A is less than B. |
| > | A > B | A is greater than B. |
| <= or =< | A <= B | A is less than or equal to B. |
| >= or => | A >= B | A is greater than or equal to B. |
| <> or >< | A <> B | A is not equal to B. |
| == | A == B | A and B will PRINT the same if they are equal to six significant digits. However, if one value prints in explicit notation and the other value prints in E format notation, the relation will always be false. |
Operators in string relational expressions determine how BASIC compares strings. BASIC determines the value of each character in the string by converting it to its ASCII value. ASCII values are listed in Appendix A. BASIC compares the strings character by character, left to right, until it finds a difference in ASCII value.
In the following example, BASIC compares A$ and B$ character by character. The strings are identical up to the third character. Because the ASCII value of Z (90) is greater than the ASCII value of C (67), A$ is less than B$. BASIC evaluates the expression A$ < B$ as true (-1) and prints "ABC comes before ABZ".
A$ = 'ABC'
B$ = 'ABZ'
IF A$ < B$
THEN PRINT 'ABC comes before ABZ'
ELSE IF A$ == B$
THEN PRINT 'The strings are identical'
ELSE IF A$ > B$
THEN PRINT 'ABC comes after ABZ'
ELSE PRINT 'Strings are equal but not identical'
END IF
END IF
END IF
END
|
If two strings of differing lengths are identical up to the last character in the shorter string, BASIC pads the shorter string with spaces (ASCII value 32) to generate strings of equal length, unless the operator is the double equal sign (==). If the operator is the double equal sign, BASIC does not pad the shorter string.
In the following example, BASIC compares "ABCDE" to "ABC " to determine which string comes first in the collating sequence. "ABC " appears before "ABCDE" because the ASCII value for space (32) is lower than the ASCII value of D (68). Then BASIC compares "ABC " with "ABC" using the double equal sign and determines that the strings do not match exactly without padding. The third comparison uses the single equal sign. BASIC pads "ABC" with spaces and determines that the two strings match with padding.
A$ = 'ABCDE'
B$ = 'ABC'
PRINT 'B$ comes before A$' IF B$ < A$
PRINT 'A$ comes before B$' IF A$ < B$
C$ = 'ABC '
IF B$ == C$
THEN PRINT 'B$ exactly matches C$'
ELSE PRINT 'B$ does not exactly match C$'
END IF
IF B$ = C$
THEN PRINT 'B$ matches C$ with padding'
ELSE PRINT 'B$ does not match C$'
END IF
|
Output
B$ comes before A$ B$ does not exactly match C$ B$ matches C$ with padding |
Table 1-11 shows how relational operators work in string relational expressions.
| Operator | Example | Meaning |
|---|---|---|
| = | A$ = B$ | Strings A$ and B$ are equal after the shorter string has been padded with spaces to equal the length of the longer string. |
| < | A$ < B$ | String A$ occurs before string B$ in ASCII sequence. |
| > | A$ > B$ | String A$ occurs after string B$ in ASCII sequence. |
| <= or =< | A$ <= B$ | String A$ is equal to or precedes string B$ in ASCII sequence. |
| >= or => | A$ >= B$ | String A$ is equal to or follows string B$ in ASCII sequence. |
| <> or >< | A$ <> B$ | String A$ is not equal to string B$. |
| == | A$ == B$ | Strings A$ and B$ are identical in composition and length, without padding. |
A logical expression can have one of the following formats:
Logical expressions are valid only when the operands are integers. If the expression contains two integer operands of differing data types, the resulting integer has the same data type as the higher integer operand. For example, the result of an expression that contains a BYTE integer and a WORD integer would be a WORD integer. Table 1-12 lists the logical operators.
| Operator | Example | Meaning |
|---|---|---|
| NOT | NOT A% | The bit-by-bit complement of A%. If A% is true (-1), NOT A% is false (0). |
| AND | A% AND B% | The logical product of A% and B%. A% AND B% is true only if both A% and B% are true. |
| OR | A% OR B% | The logical sum of A% and B%. A% OR B% is false only if both A% and B% are false; otherwise, A% OR B% is true. |
| XOR | A% XOR B% | The logical exclusive OR of A% and B%. A% XOR B% is true if either A% or B% is true but not if both are true. |
| EQV | A% EQV B% | The logical equivalence of A% and B%. A% EQV B% is true if A% and B% are both true or both false; otherwise the value is false. |
| IMP | A% IMP B% | The logical implication of A% and B%. A% IMP B% is false only if A% is true and B% is false; otherwise, the value is true. |
The truth tables in Figure 1-2 summarize the results of these logical operations. Zero is false; -1 is true.
Figure 1-2 Truth Tables
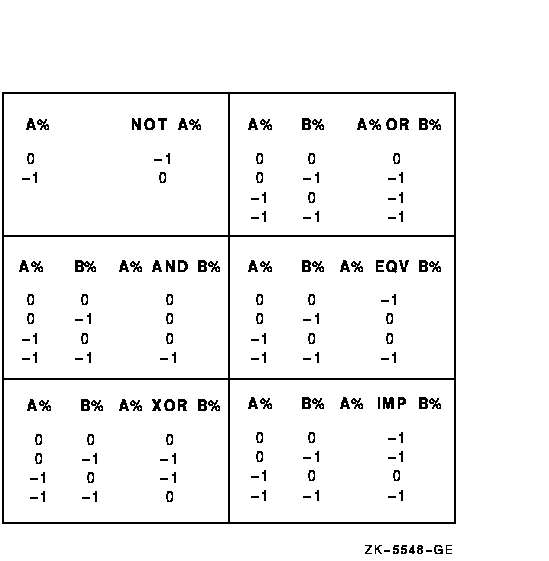
The operators XOR and EQV are logical complements.
BASIC determines whether the condition is true or false by testing the result of the logical expression to see whether any bits are set. If no bits are set, the value of the expression is zero and it is evaluated as false; if any bits are set, the value of the expression is nonzero, and the expression is evaluated as true. However, logical operators can return unanticipated results unless -1 is specified for true values and zero for false.
In the following example, the values of A% and B% both test as true because they are nonzero values. However, the logical AND of these two variables returns an unanticipated result of false.
A% = 2%
B% = 4%
IF A% THEN PRINT 'A% IS TRUE'
IF B% THEN PRINT 'B% IS TRUE'
IF A% AND B% THEN PRINT 'A% AND B% IS TRUE'
ELSE PRINT 'A% AND B% IS FALSE'
END
|
Output
A% IS TRUE B% IS TRUE A% AND B% IS FALSE |
The program returns this seemingly contradictory result because logical operators work on the individual bits of the operands. The 8-bit binary representation of 2% is as follows:
0 0 0 0 0 0 1 0 |
The 8-bit binary representation of 4% is as follows:
0 0 0 0 0 1 0 0 |
Each value tests as true because it is nonzero. However, the AND operation on these two values sets a bit in the result only if the corresponding bit is set in both operands. Therefore, the result of the AND operation on 4% and 2% is as follows:
0 0 0 0 0 0 0 0 |
No bits are set in the result, so the value tests as false (zero).
If the value of B% is changed to 6%, the resulting value tests as true (nonzero) because both 6% and 2% have the second bit set. Therefore, BASIC sets the second bit in the result and the value tests as nonzero and true.
The 8-bit binary representation of -1 is as follows:
| Previous | Next | Contents | Index |